Sequences - Finding a Rule

To find a missing number in a Sequence, first we must have a Rule

Sequence

A Sequence is a ready of things (normally numbers) that are in order.

Sequence

Each number in the sequence is called a term (or sometimes "chemical element" or "member"), read Sequences and Series for a more in-depth give-and-take.

Finding Missing Numbers

To find a missing number, first find a Dominion behind the Sequence.

Sometimes we tin just wait at the numbers and see a pattern:

Example: 1, iv, 9, 16, ?

Answer: they are Squares (i2=1, 22=4, 32=nine, 42=sixteen, ...)

Dominion: tenn = n2

Sequence: one, 4, nine, sixteen, 25, 36, 49, ...

Did you run into how we wrote that rule using "x" and "n" ?

tenn means "term number northward", so term 3 is written ten3

And nosotros can calculate term iii using:

x3 = iiiii = 9

Nosotros tin utilise a Rule to find any term. For example, the 25th term tin can exist found by "plugging in" 25 wherever due north is.

x25 = 25ii = 625

How almost some other example:

Case: three, 5, 8, thirteen, 21, ?

Afterward 3 and v all the rest are the sum of the two numbers before,

That is 3 + 5 = viii, 5 + 8 = xiii etc, which is part of the Fibonacci Sequence:

iii, 5, 8, 13, 21, 34, 55, 89, ...

Which has this Rule:

Dominion: xn = xn-1 + xn-ii

At present what does xn-1 mean? It means "the previous term" as term number northward-1 is 1 less than term number north.

And xnorth-2 ways the term earlier that ane.

Let's try that Rule for the sixth term:

106 = ten6-ane + ten6-ii

ten6 = x5 + ten4

And so term 6 equals term 5 plus term iv. We already know term five is 21 and term 4 is thirteen, so:

x6 = 21 + 13 = 34

Many Rules

One of the troubles with finding "the next number" in a sequence is that mathematics is so powerful we can find more than than one Rule that works.

What is the next number in the sequence 1, 2, 4, seven, ?

Here are three solutions (at that place tin exist more!):

Solution 1: Add together 1, and so add together 2, 3, 4, ...

So, ane+ane=ii, ii+ii=4, 4+3=7, 7+four=11, etc...

Rule: 10n = n(n-1)/2 + one

Sequence: ane, 2, 4, seven, 11, 16, 22, ...

(That rule looks a bit complicated, but it works)

Solution 2: After 1 and two, add the 2 previous numbers, plus 1:

Rule: xn = xn-one + xn-2 + 1

Sequence: 1, 2, 4, 7, 12, 20, 33, ...

Solution three: After 1, 2 and four, add together the three previous numbers

Rule: tennorthward = xn-1 + 10n-2 + tenn-three

Sequence: i, 2, four, 7, 13, 24, 44, ...

So, we take three perfectly reasonable solutions, and they create totally different sequences.

Which is right? They are all right.

And there are other solutions ...

race

... it may exist a list of the winners' numbers ... so the next number could exist ... anything!

Simplest Rule

When in doubt choose the simplest rule that makes sense, but besides mention that there are other solutions.

Finding Differences

Sometimes it helps to find the differences between each pair of numbers ... this tin often reveal an underlying pattern.

Here is a elementary case:

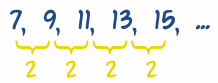
sequences first differences

The differences are always 2, so we can estimate that "2n" is function of the answer.

Let u.s.a. try 2n:

n: 1 2 3 iv v
Terms (xn): 7 ix 11 thirteen 15
2n: 2 iv vi 8 x
Incorrect by: 5 5 5 5 five

The concluding row shows that we are ever wrong by 5, and so just add 5 and we are done:

Rule: xnorthward = 2n + 5

OK, we could have worked out "2n+5" by just playing effectually with the numbers a bit, but we desire a systematic style to practice it, for when the sequences go more than complicated.

Second Differences

In the sequence {1, two, four, 7, 11, 16, 22, ...} we need to discover the differences ...

... and so find the differences of those (called 2d differences), like this:

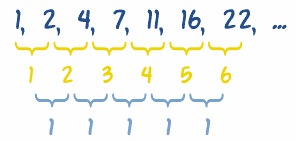
sequences second differences

The second differences in this case are 1.

With second differences we multiply past northward2 two

In our instance the difference is 1, so permit us attempt just n2 2 :

n: 1 2 3 four 5
Terms (xdue north): 1 2 4 7 11
ntwo 2 : 0.v 2 4.5 8 12.5
Wrong by: 0.5 0 -0.5 -one -1.5

Nosotros are close, but seem to be drifting by 0.5, then allow usa try: ntwo 2 − n ii

nii two − north 2 0 1 three six 10
Wrong by: 1 ane i 1 1

Incorrect by 1 now, so allow us add 1:

ntwo 2 − due north 2 + 1 i 2 iv vii eleven
Wrong by: 0 0 0 0 0

We did it!

The formula n2 ii − north two + ane can be simplified to n(due north-i)/ii + 1

So by "trial-and-error" we discovered a rule that works:

Dominion: xn = n(north-1)/two + ane

Sequence: 1, 2, 4, 7, xi, 16, 22, 29, 37, ...

Other Types of Sequences

Read Sequences and Serial to larn about:

  • Arithmetic Sequences
  • Geometric Sequences
  • Fibonacci Sequence
  • Triangular Sequence

And there are too:

  • Prime Numbers
  • Factorial Numbers

And many more!

In truth in that location are too many types of sequences to mention here, only if there is a special one you would similar me to add just let me know.